ЛЕКЦИЯ 3

Вакуумные черенковские СВЧ-приборы

1. Электромагнитные волны в волноводах.

В свободном пространстве электромагнитные волны распространяются в виде плоских волн, т.е. в данный момент существует плоскость, на которой напряженность электрического поле – Е и индукция магнитного поля – В постоянны. Эта плоскость называется фронтом волны. Зависимость Е и В от времени и координаты – z, вдоль которой распространяется волна, имеет вид

Е = Е₀ sin (wt – kz) (1)

B = B₀ sin (wt - kz)

Величина k называется волновым числом, причем k = 2p / l, где l - длина волны. Величинa w / k называется фазовой скоростью волны – это скорость распространения фронта волны. В вакууме w = kс, где с – скорость света, с = 3 @10⁸ м/с. Эти волны называются поперечными, так как .

Пусть теперь волна распространяется в металлической трубе. Ещё раз напомним, что мы рассматриваем диапазон частот, который называется СВЧ-диапазоном, аббревиатура СВЧ означает сверхвысокие частоты. Этот диапазон частот располагается от частоты 1 ГГц до 1000 ГГц, или соответственно от длины волны l = 30 см до l = 0,3 мм.

На этих частотах, как это следует из лекции 2, электромагнитное поле проникает в металл на малую глубину. Поэтому, если на вход трубы подаётся СВЧ-излучение, то оно за пределы трубы выйти не может и волна будет распространяться вдоль оси трубы – z. Но при этом в стенках трубы, который называется волноводом, возникают токи, которые приводят к отражению волны и пространственная структура волны отличается от структуры плоской волны.

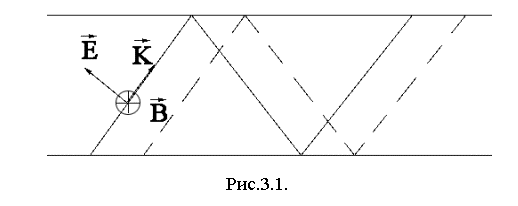
Из этого рисунка следует, что в волноводе Е – поле может иметь компоненту вдоль оси волновода. Волна распространяется вдоль вектора k, который можно разложить на две компоненты k_^ и k_z, (k_^² + k_z²) = k². Поскольку волна распространяется в вакууме, то w = k с. Из-за интерференции волны отражённой от нижней стенки с волной отражённой от верхней стенки (рис.3.1) зависимость амплитуды колебаний электрического и магнитного поля в поперечном направлении будет иметь периодический характер. В наиболее простом случае волновода прямоугольного сечения эти зависимости от поперечной координаты имеют вид

Е_y - sin k_x x (2)

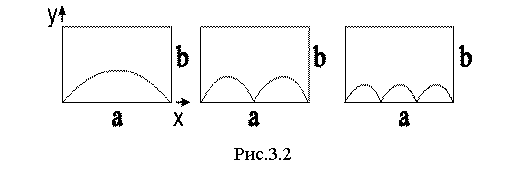
Такая структура волны возникает из-за отражений компоненты поля Е_y от стенок b. Компонента поля Е_y на стенках b должна быть равна нулю. Т.е. в направлении x наблюдается структура стоячей волны. Три различные распределения, приведённые на рисунке 3.2, соответствуют трём различным типам мод с трёмя различными значениями k_x: p / a, 2p / a, 3p /a. При k_x = p / a в направлении x укладывается половина длины волны. Отсюда следует, что при выполнении условия l / 2 > a волна по волноводу распространяться не может. Если размер b достаточно мал b < l /2, то компонента поля Е_y не будет зависеть от y. Если b > l /2, то возможно возникновение стоячей волны и в направлении y. В общем случае

Е_y -  sin k_x x cos k_yy, (3)

где k_x = m p /a, а k_y = n p /b. Существует множество волн Е_mn (E₁₁, E₂₁, E₃₁, E₃₂ ...).

В круглом волноводе также существует множество собственных мод E_nm (Е₀₁, Е₀₂, Е₁₁, Е₁₃....); периодичность в направлении f указывает индекс- n, в направлении r ® m. На стенках волновода должны быть выполнены граничные условия. В частности, компоненты поля Е_z и E_f параллельные стенкам должны быть равны нулю, т.е. на стенке электрическое поле или равно нулю или строго перпендикулярно.

Итак, индексы у моды Е_nm означают периодичность полей в поперечном направлении. Но кроме мод Е_nm существуют моды Н_nm. Е-моды кроме поперечных компонент поля обязательно имеют также и компоненту вдоль оси волновода. В Н-модах продольная компонента электрического поля равна нулю. Черенковские приборы основаны на торможении электронов в продольном направлении, поэтому нас в дальнейшем будут интересовать Е-моды.

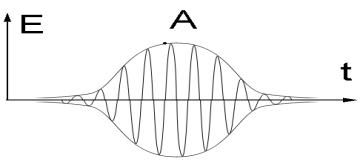
До сих пор мы полагали, что волна характеризуется определенными заданными значениями частоты и волнового вектора. На самом деле из-за конечности отрезка времени, в течение которого наблюдается волна, и из-за конечности пространства, в котором наблюдается волна, волновой процесс всегда описывается набором волн с разными значениями частот и волновых векторов. Пусть, например, электромагнитное излучение с частотой w включается на время T >> 2p/w. Тогда в среде будет распространяться сигнал, изображённый на рис 3.3.

Рис.3.3.

Его спектр состоит из нескольких гармоник с частотами близкими к w. Возникает вопрос: с какой скоростью будет перемещаться этот сигнал в пространстве?

Для простоты рассмотрим частный пример, когда волновой процесс состоит из двух волн с равной амплитудой, с двумя близкими значениями частот w₀ ‑ dw и w₀ + dw (dw << w₀) и с близкими значениями волновых векторов k₀ ‑dk и k₀ + dk (dk << k₀).

Уравнение для суммарного значения поля этих волн запишется в виде:

E = E₀ sin ((w₀ ‑ dw) t – (k₀ ‑dk) z) +E₀ sin ((w₀ + dw) t – (k₀ +dk) z) =

2 E₀ cos (dw t – dk z) sin (w₀ t – k₀ z)

Зависимость напряжённости поля E от z в данный момент времени изображёна на рис. 3.4.

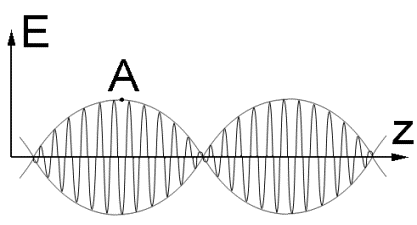
Рис.3.4

Приблизительно можно сказать, что это график синусоиды с периодом 2p / k₀ и с медленно меняющейся амплитудой. Период изменения амплитуды равен 2p /  dk. Скорость перемещения в пространстве амплитуды этого сигнала, обозначенного т. А на рис 3.4., найдётся из равенства dw t – dk z = 0. Дифференцируя это равенство находим w = dz / dt = dw / dk. Величина w называется групповой скоростью сигнала электромагнитных волн. При распространении сигнала электромагнитных волн в свободном пространстве справедливо равенство w = k c, где с – константа, равная скорость света. Когда w  не зависит от  k , говорят, что среда не имеет дисперсии. В этом случае фазовая и групповая скорости волн равны, т. е. w / k = dw / dk .

2. Дисперсия вакуумного волновода

Дисперсионной кривой называется зависимость w(k_z). Для волновода зависимость w(k_z) имеет вид w² = k² c² = с² (k_^² + k_z²).

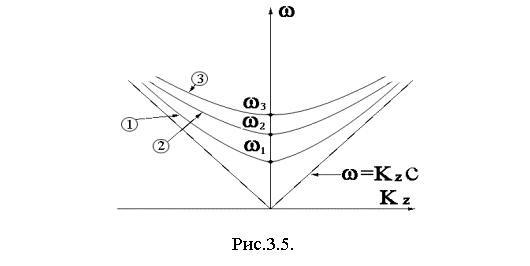
В свободном пространстве фазовая скорость постоянна и равна с. Прямая линия w = k_z c соответствуют этой волне, распространяющейся вдоль направления z. Различные кривые соответствуют различным модам волновода. Видно, что на каждой кривой фазовая скорость v_ф = w / k_z не постоянна. При k_z = 0, v_ф ® ¥, а при k_z ® ¥ v_ф ® c и всегда v_ф > c. Частоты w₁, w₂, w₃ называются критическими частотами для каждой из мод. На этих частотах k_z = 0, т.е. волна вдоль оси z не распространяется. Из этого рисунка следует, что электромагнитное излучение на частоте меньше, чем w₁ распространяться не может. Эта частота определяется только геометрическими размерами волновода, в случае цилиндра, например, определяется его радиусом. Т.е. в волноводе данного радиуса могут распространяться только волны с частотой волны большей, чем критическая частота w₁. В диапазоне частот w₁ < w <w₂ может распространяться только низшая мода – кривая 1. Поперечная структура при изменении частоты от w₁ до w₂ изменяться не может. Если w₂ <w < w₃, то можно возбудить только моду 1 или только моду 2, или моды 1 и 2 вместе. В таком случае говорят, что волновод стал сверхразмерным – в нем могут распространяться несколько мод.

Групповая скорость волн dw / dk  в волноводе, как видно из рис.3.5, не постоянна. При малых k_z, т.е. при частотах близких к критическим, групповая скорость близка к нулю. Это означает, что скорость распространения энергии сигнала электромагнитных волн мала. При больших k_z групповая скорость волн стремится к скорости света. Таким образом, отношение фазовой и групповой скоростей в волноводе для разных значений k_z сильно меняется, но направление этих скоростей всегда совпадает. Как мы увидим позже, возможна ситуация, когда направления этих скоростей не совпадают.

2. Эффект Черенкова.

Пусть электромагнитная волна имеет компоненту Е_z электрического поля вдоль направления распространения – z. Такая волна не может существовать в свободном пространстве, но может распространяться в волноводе или в некоторых средах.

Рассмотрим воздействие такой волны на покоящийся электрон. Электрон окажется в переменном электрическом поле и будет совершать колебательное движение вдоль оси z со скоростью

(4)

Среднее по времени значение скорости равно нулю. Пусть теперь электрон движется вдоль оси z, со скоростью малой по сравнению с фазовой скоростью волны. Тогда опять на длине взаимодействия L >> l скорость электрона под действием поля не изменится.

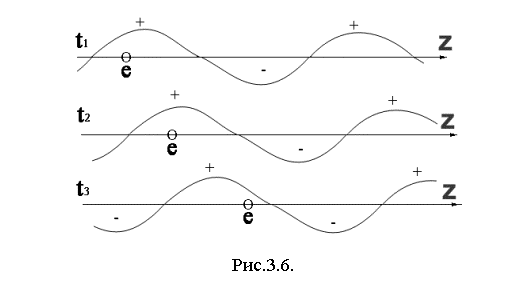
Пусть теперь электрон движется из точки z₁ в точку z₂ (z₂-z₁ = L) со скоростью равной фазовой скорости волны. На рисунке 3.6. показано распределение продольной компоненты поля E_z вдоль оси z в различные моменты времени t₁, t₂, и t₃. Если электрон в момент времени t₁ попал в ускоряющую фазу (рис.3.6.), то он будет ускоряться и в моменты времени t₂ и t₃, до тех пор, пока за счет разности скоростей электрона и волны он не попадёт в другую фазу волны. Длина, на которой происходит ускорение может значительно превышать длину волны, L >> l.

На этом принципе может работать ускоритель частиц. Процесс ускорения заканчивается, когда электрон попадает в тормозящую фазу волны, за счет того, что его скорость стала больше фазовой скорости волны. Можно сделать так, чтобы фазовая скорость волны возрастала вдоль направления движения электрона (например, за счёт изменения поперечных размеров волновода), тогда процесс ускорения электрона может происходить долго.

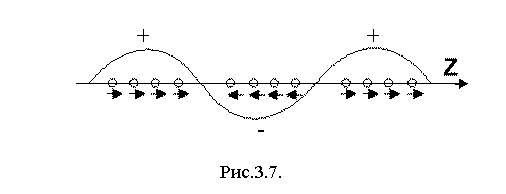
Теперь пусть на вход волновода длиной L поступает пучок электронов со скоростью равной фазовой скорости волны. Тогда электроны пучка, попавшие на входе волновода в ускоряющую фазу, будут ускоряться, а электроны в замедляющей фазе замедляться. В результате на некоторой длине взаимодействия все электроны соберутся в сгустки, которые будут двигаться в фазе волны, где электрическое поле равно нулю.

В результате энергия от пучка к волне передаваться не будет, работа поля над электронами равна нулю. Если же скорость электронов превышает фазовую скорость волны, то на некоторой длине сгустки электронов будут формироваться в фазе замедляющего поля. Некоторое время после образования сгустка все электроны пучка будут двигаться в тормозящей фазе и передавать свою энергию волне. Затем начнется обратный процесс передачи энергии от волны к пучку. Таким образом, если скорость пучка превышает фазовую скорость волны, и длина взаимодействия специально подобрана, то возможна передача энергии от пучка к волне. Это и есть эффект Черенкова, он происходит, если

v_b ³ v_ф т.е. v_b ³ w/k_z или w # k_zv_b (5)

В гладком вакуумном металлическом волноводе могут распространяться волны только с фазовой скоростью большей скорости света, такие волны называются быстрыми. Так как скорость электронов всегда меньше скорости света, то эффект Черенкова в этом случае не возможен.

3. Вакуумные черенковские приборы ЛБВ и ЛОВ.

Однако существуют металлические волноводы, в которых волны распространяются с фазовой скоростью меньшей, чем скорость света. Одним из таких волноводов является гофрированный волновод

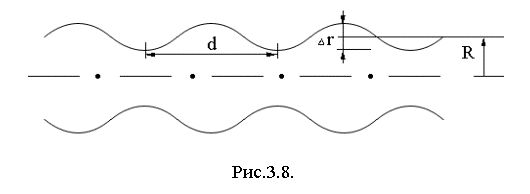
Если гофрировка не очень велика (Dr / R<< 1), то дисперсия этого волновода будет похожа на дисперсию волн гладкого цилиндрического волновода. Оказывается, поле волны в таком волноводе можно представить в виде суммы полей волн гладкого волновода (которая переносит основную энергию) и медленной волны, т.е.

Е_z = E_z⁰ sin(wt-k₀z) + Е_z¹ sin(wt-k¹z) + E_z² (6)

В этом выражении Е_z¹ << E_z⁰. Итак, если бы волновод был гладкий, то поле в волноводе на частоте w было равно Е_z = E_z⁰ sin(wt-k₀z). Если же его стенка гофрирована, то к этому полю добавляется поле с другим волновым вектором k¹ (т.е. с другой фазовой скоростью). Дисперсия гофрированного волновода показана на рис.3.9.

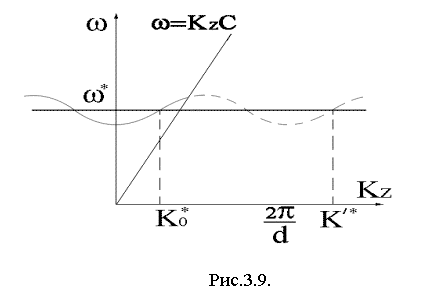
Сплошная линия приблизительно соответствует быстрой моде гладкого волновода с полем E⁰. Пунктирная линия соответствует медленной компоненте поля Е¹ гофрированного волновода. Если теперь подобрать энергию электронов пучка, так чтобы скорость электронов равнялась фазовой скорости медленной волны, то пучок может передать энергию волне на конечном участке волновода.

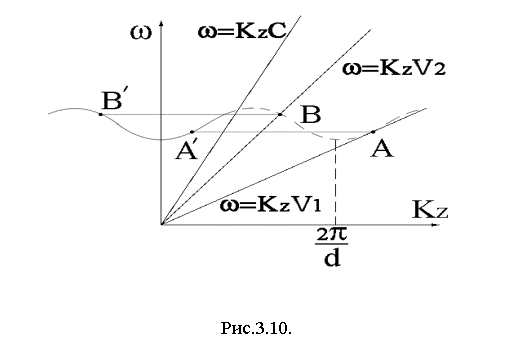
Если скорость электронов такова, что линия w = k_zv, где v – скорость электронов, пересекает дисперсионную кривую в точке А, то пучок будет взаимодействовать с медленной гармоникой волны гофрированного волновода с частотой и волновым вектором соответствующими точке А. При этом будет возбуждаться и основная (быстрая) гармоника с частотой и волновым вектором соответствующими точке А¹. Обе гармоники возбуждаемой волны на частоте w имеют положительную фазовую скорость. Групповая скорость обеих гармоник также положительна dw / dk_z > 0, т.е. энергия волны будет переноситься в направлении движения электронов. Таким образом, если через левый торец гофрированного волновода влетает электронный пучок и в этот же торец подается СВЧ-волна на частоте w, то на конечном участке волновода напряженность поля этой волны может увеличиваться. Прибор, работающий на этом принципе, называется лампой бегущей волны или ЛБВ. Еще раз подчеркнем, что взаимодействие электронов происходит только с полем медленной волны Е_z¹, но при этом увеличивается и напряженность полей быстрой волны Е⁰. Если все излучение полностью уходит из отрезка волновода, то этот прибор может работать только как усилитель. Если же часть энергии отражается от правого конца волновода и от левого, то этот прибор может работать как генератор. Это происходит так. В результате взаимодействия с пучком электрическое поле волны на входе Е_z^left к выходу возрастает по экспоненциальному закону с коэффициентом усиления dk

Е_z = Е_z^left e^dkL

Пусть от правого торца отразится часть волны k₁, тогда

Е₀^отраж = k₁ Е_z^left e^dkL

Затем после отражения от левого конца с коэффициентом отражения k₂. возникает волна вдоль направления скорости электронов с полем

Е^отраж = k₁ k₂ Е_z^left e^dkL

Если величина k₁ k₂ е^dkL > 1, то такое устройство может начать работать как генератор. Причем поле Е_z^left на частоте w может возникнуть случайно, например, из-за шумов системы.

Вернемся к рис.3.10, если линия w = k_z v пересекает дисперсионную кривую в т. В, то может возбуждаться медленная гармоника на частоте и волновом векторе соответствующими точке В. Эта гармоника имеет положительную фазовую скорость, но отрицательную групповую скорость, т. е. энергия будет переносится навстречу пучку. Одновременно будет возбуждаться быстрая гармоника на частоте и волновом векторе соответствующими точке В¹. Её групповая скорость также отрицательна. Таким образом, энергия волны распространяется навстречу пучку, т.е. обратная связь осуществляется автоматически. Такой прибор называется лампой обратной волны – ЛОВ.

Лампа обратной волны с замедляющей системой в виде гофра носит название карсинотрон. Именно карсинотрон был выбран для первого в мире эксперимента по релятивистской СВЧ электронике (совместный эксперимент Института прикладной физики, Нижний Новгород и Института общей физики, Москва, 1973 год). Дело в том, что у этого прибора нет высоких требований к моноэнергетичности электронного пучка. Это было важно в первых экспериментах, поскольку форма импульса напряжения на катоде имела форму колокола, т. е. энергия электронов в течение импульса существенно изменялась. В карсинотроне при этом не исчезает обратная связь, может только в течение импульса изменяться частота генерации.

4. Управление частотой излучения

Сначала рассмотрим СВЧ-генератор. Если изменять скорость электронов, то точка В будет двигаться по дисперсионной кривой медленной волны, т.е. частота генератора будет перестраиваться. Из рис.3.10. следует, что диапазон перестройки частоты ограничен тем, что частоты медленной волны ограничены w_min < w < w_max. Кроме того, уменьшая скорость электронов, за счёт уменьшения энергии электрона при влёте в лампу eU мы уменьшаем мощность пучка Р = еU×I_b. Поэтому трудно получить неизменную выходную мощность при изменении U. Новые проблемы возникают при использовании релятивистских пучков. Здесь при значительном изменении энергии электронов, скажем, от 500 кэВ до 700 кэВ скорость электронов меняется незначительно от 2,59×10¹⁰ см/с до 2,72×10¹⁰ см/с.

Важной характеристикой усилителя является полоса усиления, т.е. диапазон частот, который может усиливаться с постоянным коэффициентом усиления. Широкая полоса усиления достигается в случае, если дисперсионная кривая почти параллельна линии w = k_z v в широком частотном диапазоне. В этом случае черенковское условие w ³ k_z v выполняется не в одной точке, а в некотором диапазоне частот. Такая ситуация реализуется в ЛБВ при осуществлении резонанса в т. А рис. 3.10.